随机游走
A drunk man will find his way home, but a drunk bird may get lost forever.
本文使用几乎纯组合的方法证明低维随机游走的几个有趣的结论,即一维与二维随机游走的回返性与三维游走的非回返性。
一维随机游走
一维随机游走的定义非常简单:一个动点在每一个时刻 \(n = 1, 2, \dots, 3\) 以概率 \(p\) 向上移动一格,以概率 \(q = 1 - p\) 向下移动一格。当 \(p = q=\frac{1}{2}\) 时,这个游走称为对称的。下面的讨论,我们对只考虑对称的情形。
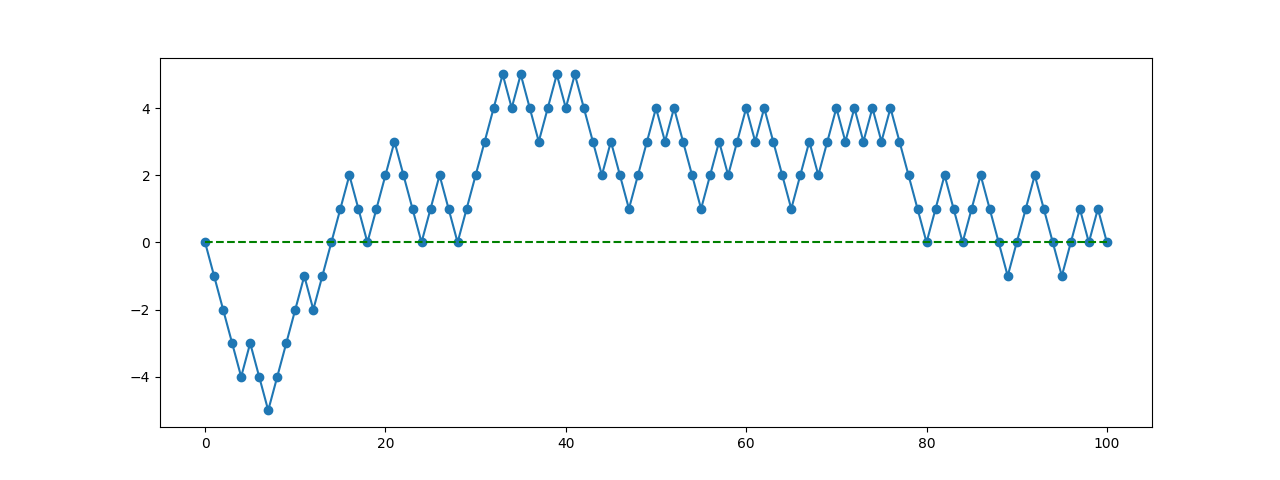
下图为随机游走中的一个时间-空间坐标系,横坐标代表时间,纵坐标代表位置,这样的一条折现就称为运动的轨迹。
组合法基础
我们以 \(L(x, y)\) 表示从原点开始到 \((x,y)\)的轨迹的条数。当 \(x, y\) 奇偶性相同且 \(y\le x\) 时,我们有
\[L(x, y) = C_x^{(x+y)/2}\]其他情形下,\(L(x,y) = 0\). (证明是显然的,即组合数定义)
下面介绍本文最重要的引理——反射原理。
反射原理 假设 \(A(x_0, y_0), B(x, y), A'(x_0, -y_0)\) 是在坐标上的点,且 \(0<x_0<x, y_0>0, y>0\),那么由 \(A\) 到 \(B\) 的与横坐标相交的路线的条数等于由 \(A'\) 到 \(B\) 的所有条数。
证明:下图的一一映射道尽一切。
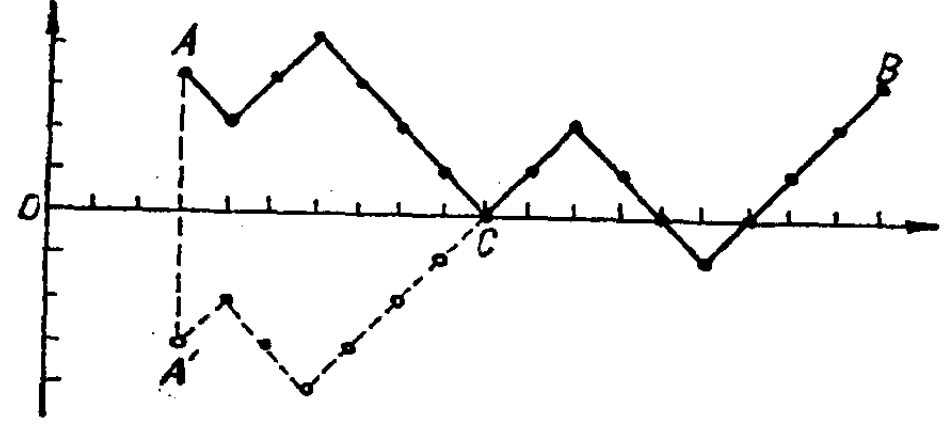
在以后的叙述中,我们称路线为正的,如果它的顶点都严格位于横坐标轴上方(除了起始点);称路线为非负的,如果它没有位于横坐标轴下方的顶点。
由反射原理我们可以得到如下推论:
引理1 以原点 \((0,0)\) 为起点,以横坐标 \(x\) 为终点的正路线的总数:1) 当 \(x\) 为偶数时,为 \(C_{x-1}^{x/2}\);2) 当 \(x\) 为奇数时,为 \(C_{x-1}^{(x-1)/2}\).
证明:首先这样的路线必通过 \((1,1)\),由 \((1,1)\) 到达横坐标 \(x\) 的路线总数为 \(\sum_{y=y_0}^xL(x-1, y-1)\), 由 \((1, -1)\) 到达横坐标 \(x\) 的路线总数为 \(\sum_{y=y_0}^{x-2}L(x-1, y+1)\), 其中
\[y_0 = \begin{cases} 1, & x \text{为奇数} \\ 2, & x \text{为偶数} \end{cases}\]注意求和时 \(y\) 的取值范围,如果是 \((1,-1)\) 开始上界只能到 \(x-2\)。
由反射原理我们知道正路线即为他们的差,也就是
\[\sum_{y=y_0}^xL(x-1, y-1) -\sum_{y=y_0}^xL(x-1, y+1) = L(x-1, y_0-1) = \begin{cases} C_{x-1}^{(x-1)/2}, & x \text{为奇数} \\ C_{x-1}^{x/2}, & x \text{为偶数} \end{cases}\]一个显然的推论是,以原点 \((0,0)\) 为起点,以横坐标 \(x\) 为终点的正路线和负路线的总数为两倍的正路线,为 \(2C_{2n-1}^n=C_{2n}^n\),若 \(x=2n\);为 \(2C_{2n}^n\),若 \(x=2n+1\).
一维随机游走的回返性
有了最重要的反射原理及其推论,我们就可以证明一维随机游走的回返性了,即动点在运动后终能回到原点的概率为 \(1\).
在考虑这一问题的时候,我们只考虑偶数步回到零的可能,即 \((0,0)\) 到 \((2n, 0)\) 的路线数。 我们以 \(u_{2n}\) 表示动点在第 \(2n\) 步时回到原点的概率,由路线数与总路线数之比可立即推得:
\[u_{2n} = \frac{C_{2n}^n}{2^{2n}}\]其次,以 \(f_{2n}\) 表示动点在 \(2n\) 时 第一次 回到原点的概率,我们有如下引理:
引理2 \(f_{2n} = u_{2n-2} - u_{2n}\) 即第一次回到原点的概率等于在第 \(2n\) 步回到原点的概率减去在第 \(2n-2\) 步回到原点的概率。
证明:我们引入 \(A_{2n}\):在 \(2n\) 步之内,动点一次也未返回原点,也就是正路线和负路线;\(B\) 质点于第 \(2n\) 步返回原点。由上一节的推论我们立刻知道
\[P(A_{2n}) = u_{2n}\]我们知道 \(A_{2n-2}\bigcap B\) 表示在第 \(2n\) 步首次返回原点,因此 \(P(A_{2n-2}\bigcap B) = f_{2n}\).
易知 \((A_{2n-1}\bigcap B)\bigcup(A_{2n-2}\bigcap \bar{B}) = A_{2n-2}\),而从定义我们可以看到 \(2n\) 步不返回原点的事件数就是 \(2n-2\) 步不返回原点的事件交上 \(2n\) 步不返回原点的事件,也就是 \(A_{2n-2}\bigcap\bar{B}=A_{2n}\),因此
\[\begin{array} P(A_{2n-2}\bigcap B) + P(A_{2n}) &= P(A_{2n-2}) \\ f_{2n} + u_{2n} &= u_{2n-2} \\ f_{2n} &= u_{2n-2} - u_{2n} \end{array}\]有了这一引理,我们立刻可以知道动点在 \(2n\) 步之内返回原点的概率为 \(f_2 + f_4+\dots+f_{2n} = 1 - u_2 - u_4 - \dots - u_{2n} = 1 - u_{2n}\).
而斯特林公式告诉我们对于 \(u_{2n}\) 的估计:
\[\begin{array} nn! &\approx \sqrt{2\pi n}(\frac{n}{e})^n \\ C_{2n}^n &\approx 2^{2n}\sqrt{\frac{2}{\pi n}} \\ u_{2n} &\approx \frac{1}{\sqrt{\pi n}} \end{array}\]也就有如下定理:
定理1 一维随机游走的回返性:动点以概率 \(1\) 返回原点。
除了回返性,随机游走还有许多重要的性质,例如对于动点逗留时间讨论导出的反正弦定理,限于篇幅,这里不再赘述。
二维与三维随机游走
一维随机游走可以自然的推广到更高的维度:二维即在平面上以 \(\frac14\) 的概率向上、下、左、右移动一格;三维即在空间中以 \(\frac16\) 的概率向上、下、左、右、前、后移动一格。
首先证明一条引理:
引理3 \(u_{2n} = \sum_{k=1}^n f_{2k}u_{2n-2k}\)
证明:由全概率公式和对于 \(u, f\) 的定义不难推得。
有了这一引理,我们对左右两边求和:
左式: \(\sum_{n=1}^\infty u_{2n} = \sum_{n=0}^\infty u_{2n} -1\).
右式:\(\sum_{n=1}^\infty[\sum_{k=1}^n f_{2k}u_{2n-2k}] = \sum_{k=1}^\infty f_{2k}\sum_{n=0}^\infty u_{2n}\). (?)
因此
\[\begin{array} \sum\sum_{n=0}^\infty u_{2n}-1 &= \sum_{n=1}^\infty u_{2n} -1 =\sum_{k=1}^\infty f_{2k}\sum_{n=0}^\infty u_{2n} \\ \sum_{n=1}^\infty f_{2n} &= 1 - \frac1{\sum_{n=0}^\infty u_{2n}} \end{array}\]所以我们立刻得到:若级数 \(\sum u_{2n}\) 发散,那么 \(\sum f_{2n} = 1\),即回到原点的概率为 \(1\). 反之,则回到原点的概率小于 \(1\).
首先在二维随机游走中,我们求概率 \(u_{2n}\), 总路线有 \(4^{2n}\) 条,而回到原点则要求向上和向下的路线数相等,向左和向右的路线数相等,因此这样的路线为:
\[\sum_{k=0}^n\frac{(2n)!}{k!k!(n-k)!(n-k)!} = C_{2n}^n\sum_{k=0}^n (C_n^k)^2 = (C_{2n}^n)^2\]那么同样利用斯特林公式:
\[u_{2n} = 4^{-2n}(C_{2n}^n)^2\approx \frac{1}{\pi n}\]显然 \(\sum_{n=2}^\infty u_{2n} = \infty\),这是一个经典的发散级数,故二维随机游走是回返的。
而在三维随机游走中,我们有类似的:
\[u_{2n} = 6^{-2n}\sum_{0\le i + j \le n}\frac{(2n)!}{i!i!j!j!(n-i-j)!(n-i-j)!}\](以下省略一波暴算和估计)
可以得到 \(u_{2n} 的数量级为 \frac{1}{n^{3/2}}\),因此 \(\sum_{n=2}^\infty u_{2n} < \infty\),故三维随机游走是非回返的。经计算,回返的概率大约是 \(0.35\).
综上所述,一维随机游动的一条极好性质——回返性,在二维空间仍然成立,然而在三维及三维以上空间就不满足了。
随机游走的回返性最终与p级数的收敛性相关,这是一个非常有趣的结论。
参考资料
柯尔莫哥洛夫. 《概率论导引》. 本文主要是对其第四章内容的总结与笔记。