软件工程技术漫谈(1) —— 训练谜云

缘起

2021年, 随着深度学习日益强大(传统科研做不下去了), 小z同学也被迫加入了炼丹大军. 虽然小z之前从来没写过相关代码, 好在实验室硬件条件不错, 有8张A800GPU. 经过一番(痛苦的)环境配置和神经网络速成, 小z也成功搞定, 开始了调参大业.

好景不长, 新进组的师弟也要进行类似的科研工作, 也需要一半的卡. 如果小z只能使用一半的显存, 那么小z就需要减少一半batch size, 时间增加一倍问题倒不大, 反正闲着也是闲着. 然而在实验中, 小z发现一个大问题: 由于配置的不同, 之前调参得到的实验结果都要在新的batch size下重跑一遍, 甚至原来他以为的优化方法似乎在新的batch size下也并没有显著提升.

这是很正常的事情, 毕竟深度学习即使是完全一样的配置都有可能运行出不同的结果, 何况是修改了batch size这种影响较大的操作. 但是小z也实在不想重新跑一遍所有参数下的代码, 于是想到了一个办法, 也就是梯度累计: 每次迭代之后不立即更新参数, 而是把多个小 batch 的梯度累加起来, 然后再进行一次梯度更新. 这样既可以减少需要的显存, 又在理论上可以得到与原来相同的结果. 为了确认这件事, 小z做了个实验, 把两个batch size的loss曲线都画出来对比, 如下图所示:

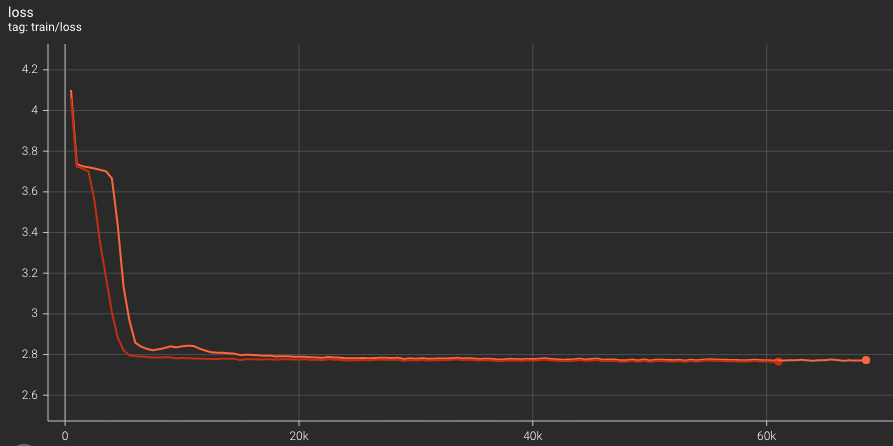
虽然最终收敛的结果区别不大, 但是开启了梯度累计时loss曲线一度明显高于没有开启的时候, 而照理来说这两条曲线应该几乎完全一致, 难道说官方的代码有bug? 出于好奇心小z还是在PyTorch平台上提出了相关的issue, 得到的解释是浮点数的舍入误差会影响计算, 所以这两条曲线都是“合理”的.

死去的关于浮点数的记忆开始攻击小z, 由于计算机硬件存储是有限的, 为了效率和可行性在存储实数时大多只存储一个近似的值, 而浮点数则是一种存储尾数和指数的方式, 广泛使用于计算机系统中, 自然也包括深度学习计算. 由于是近似的, 那么在存储和计算的过程之中就不可避免引入误差, 导致原本数学上等价的事情在浮点数世界不在等价. 例如加法的结合律在浮点数种就不再成立. 因此在比较不同有浮点数参与的算法时, 一般不会要求比特级别的相等, 而是允许一个界限(threshold).

理清这些, 确实存在一种可能: 由于开启了梯度累积时具体的计算过程和顺序不同, 导致浮点数的误差逐渐累计放大, 最终影响了整个loss. 但是这一点点浮点数的误差能累积到这个程度吗, 这个差异是能够接受的吗? 小z心里还是觉得非常疑惑, 不过反正最终收敛到的 loss 和测试集的准确率也差不多, 小z也就放下了这个疑问, 不再追问.

而在3年之后的2024年, 小z突然发现自己当时的issue被人重新提起, 而且确认了这的确是由于代码实现的bug引起的, 而不是所谓的浮点数误差. 小z大概看懂了是计算最后loss的时候需要求平均除以batch size, 而实际上代码实现的分别是 \(\frac{a}{b} + \frac{c}{d}\) 与 \(\frac{a+c}{b+d}\). 在 \(b\) 和 \(d\) 很接近, 即多次梯度下降时有效的batch size很接近时, 这两个值很接近, 也就看不出什么不同. 而当有效batch size差异很大时, loss 也就出现了较大差异. 总而言之, 这确实是代码实现的bug, 导致在使用/不使用梯度累计时的数学公式实际上是不等价的.

聪明的小z开始思考一个更深刻的问题: 这个问题更抽象一层来看是舍入误差和实现bug的分类问题. 现在存在一个标准实现(不开启梯度累积)和一个我们自己的优化实现(开启梯度累积), 在某一组输入下发现最终结果(loss)出现偏差. 由于浮点数误差的存在, 偏差是正常的, 但是这种偏差究竟是由于实现bug导致的, 还是纯粹来自于舍入误差呢?

(以上故事根据真实事件瞎编)

解决

我们今年的一项工作既是围绕这一问题展开. 正如上文所说, 我们的目标是在深度学习背景下对于误差来源的二元分类. 如果是由于舍入误差(Type-I), 开发者可以调整threshold或者使用更高精度的浮点数, 而如果是由于实现bug(Type-II), 那么开发者就应该去修复这个问题.

我们的思路是估计一个最大可能的舍入误差范围, 如下图所示: 对于我们的目标程序, 我们估计它输出可能的最大上界与最小下界. 如果参考实现的输出结果在这个界限之内, 那么我们就认为这是 Type-I 舍入误差. 反之, 我们就认为这是 Type-II 实现 bug.

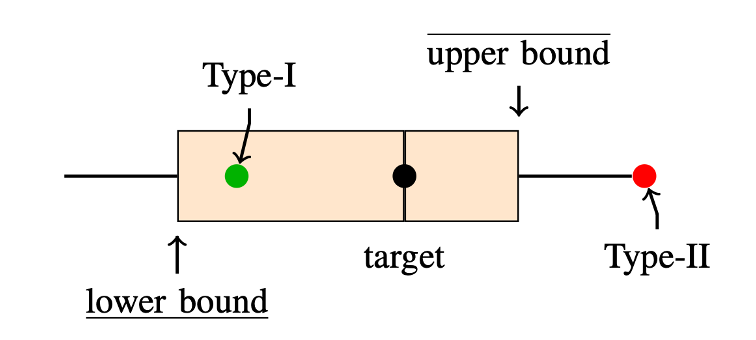
那么怎么估计一个可能的误差呢, 我们使用了古典的区间算术技术. 简单来说, 对于一个数 \(a\) 我们用一个区间 \([\underline{a}, \overline{a}]\) 来表示其可能的范围, 在原程序运行过程中, 我们用区间上的计算来动态估计每个运行结果可能的上下界. 对于加法和乘法举例如下:

\[\begin{align*} [\underline{a}, \overline{a}] + [\underline{b}, \overline{b}] & = [\underline{a} + \underline{b}, \overline{a} + \overline{b}], \\ [\underline{a}, \overline{a}] \times [\underline{b}, \overline{b}] & = [\min(\underline{ab}, \underline{a} \overline{b},\overline{a} \underline{b}, \overline{ab}), \max(\underline{a} \underline{b}, \underline{a} \overline{b}, \overline{a} \underline{b}, \overline{ab})] \end{align*}\]

而在最后, 我们自然就得到了最终输出的上下界, 与参考程序输出的比较后也就完成了分类.

(更多细节欢迎感兴趣的读者参考我们的论文)

后文

这一问题最早的提出来源于和我们组合作的企业, 他们和我讲了这个梯度累积的例子, 但是我就觉得这应该是一个挺有趣且实际的问题. 整体的技术在我看来是比较简单的, 区间算术是古典的不能再古典的技术了, 而我们是在深度学习背景下对 tensor 级别的区间计算重新发扬了一部分. 实验部分最麻烦的是数据集的收集, 因为这不像是bug检测任务有十分明确的标准和数据集, 我们在一些仓库扒了很多issue才拿到20几个数据进行验证. 虽然最后审稿时一个审稿人还是觉得我们是在做bug检测 :), 一个审稿人觉得由于条件数问题我们无法sound的估计误差:), 但他们还是慷慨的给了个大修, 也让这篇论文最后得以录用.

我以前看过jyy 老师知乎的软件工程技术漫谈, 觉得这是很不错的分享工作的模式, 这才有了本篇内容. 后续如果我们也有我个人觉得有趣的工作, 也会继续通过该方式分享.